21年全国大学生计算机应用能力与信息素养大赛

本文最后更新于：July 15, 2022 am

21年全国大学生计算机应用能力与信息素养大赛

注：此代码实现过程仅是本人初学后所敲，很多地方不足，仅供大家参考。
因为大赛结束后就没有赛题及相关介绍，这里提供给大家

1.jpg

代码如下：
1
2
3
4
5
6
7
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns

data =  pd.read_csv('C:/Users/86155/Desktop/大数据竞赛数据集_本科组.csv')
data.head()
X0 X1 X2 X3 X4 X5 X6 X7 X8 X9 X10 X11 X12 X13 X14
0 1/1/2015 Quarter1 sweing Thursday 8 0.80 26.16 1108.0 7080 98 0.0 0 0 59.0 0.940725
1 1/1/2015 Quarter1 finishing Thursday 1 0.75 3.94 NaN 960 0 0.0 0 0 8.0 0.886500
2 1/1/2015 Quarter1 sweing Thursday 11 0.80 11.41 968.0 3660 50 0.0 0 0 30.5 0.800570
3 1/1/2015 Quarter1 sweing Thursday 12 0.80 11.41 968.0 3660 50 0.0 0 0 30.5 0.800570
4 1/1/2015 Quarter1 sweing Thursday 6 0.80 25.90 1170.0 1920 50 0.0 0 0 56.0 0.800382 
1
2
3
4
5
6
7
8
import pandas as pd
data=pd.read_excel('C:/Users/86155/Desktop/xinguan.xlsx')
#plt.scatter(data['经度'],data['纬度'],
           #s=data['累计确诊'],
           #c=data['累计死亡'],cmap='Gray',
           #alpha=0.4)
#plt.grid()
data.head()
城市 累计确诊 现有疑似 累计死亡 经度 纬度
0 北京 1651 0 9 116.46 39.92
1 天津 1372 0 3 117.20 39.12
2 河北 1671 0 7 114.52 38.05
3 山西 295 0 0 112.55 37.87
4 内蒙古 1666 0 1 111.73 40.83 
1
data.info()
<class 'pandas.core.frame.DataFrame'>
RangeIndex: 1197 entries, 0 to 1196
Data columns (total 15 columns):
 #   Column  Non-Null Count  Dtype         
---  ------  --------------  -----         
 0   X0      1197 non-null   datetime64[ns]
 1   X1      1197 non-null   object        
 2   X2      1197 non-null   object        
 3   X3      1197 non-null   object        
 4   X4      1197 non-null   int64         
 5   X5      1197 non-null   float64       
 6   X6      1197 non-null   float64       
 7   X7      691 non-null    float64       
 8   X8      1197 non-null   int64         
 9   X9      1197 non-null   int64         
 10  X10     1197 non-null   float64       
 11  X11     1197 non-null   int64         
 12  X12     1197 non-null   int64         
 13  X13     1197 non-null   float64       
 14  X14     1197 non-null   float64       
dtypes: datetime64[ns](1), float64(6), int64(5), object(3)
memory usage: 140.4+ KB

1
data.isnull()
X0 X1 X2 X3 X4 X5 X6 X7 X8 X9 X10 X11 X12 X13 X14
0 False False False False False False False False False False False False False False False
1 False False False False False False False False False False False False False False False
2 False False False False False False False False False False False False False False False
3 False False False False False False False False False False False False False False False
4 False False False False False False False False False False False False False False False
... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ...
1192 False False False False False False False False False False False False False False False
1193 False False False False False False False False False False False False False False False
1194 False False False False False False False False False False False False False False False
1195 False False False False False False False False False False False False False False False
1196 False False False False False False False False False False False False False False False

1197 rows × 15 columns

1
2
#  数据类型
data.dtypes  
X0     datetime64[ns]
X1             object
X2             object
X3             object
X4              int64
X5            float64
X6            float64
X7            float64
X8              int64
X9              int64
X10           float64
X11             int64
X12             int64
X13           float64
X14           float64
dtype: object

1
2
#用中值填补Age的空缺值
data['X7']=data['X7'].fillna(data['X7'].median())
1
data.describe()
X4 X5 X6 X7 X8 X9 X10 X11 X12 X13 X14
count 1197.000000 1197.000000 1197.000000 1197.000000 1197.000000 1197.000000 1197.000000 1197.000000 1197.000000 1197.000000 1197.000000
mean 6.426901 0.729632 15.062172 1126.437761 4567.460317 38.210526 0.730159 0.369256 0.150376 34.609858 0.735091
std 3.463963 0.097891 10.943219 1397.653191 3348.823563 160.182643 12.709757 3.268987 0.427848 22.197687 0.174488
min 1.000000 0.070000 2.900000 7.000000 0.000000 0.000000 0.000000 0.000000 0.000000 2.000000 0.233705
25% 3.000000 0.700000 3.940000 970.000000 1440.000000 0.000000 0.000000 0.000000 0.000000 9.000000 0.650307
50% 6.000000 0.750000 15.260000 1039.000000 3960.000000 0.000000 0.000000 0.000000 0.000000 34.000000 0.773333
75% 9.000000 0.800000 24.260000 1083.000000 6960.000000 50.000000 0.000000 0.000000 0.000000 57.000000 0.850253
max 12.000000 0.800000 54.560000 23122.000000 25920.000000 3600.000000 300.000000 45.000000 2.000000 89.000000 1.120437 
1
2
3
4
5
#  重复值处理

#找出行重复的位置
dIndex = data.duplicated()
dIndex
0       False
1       False
2       False
3       False
4       False
        ...  
1192    False
1193    False
1194    False
1195    False
1196    False
Length: 1197, dtype: bool

1
#  可以看出没有重复值
1
data.head()
X0 X1 X2 X3 X4 X5 X6 X7 X8 X9 X10 X11 X12 X13 X14
0 1/1/2015 Quarter1 sweing Thursday 8 0.80 26.16 1108.0 7080 98 0.0 0 0 59.0 0.940725
1 1/1/2015 Quarter1 finishing Thursday 1 0.75 3.94 1039.0 960 0 0.0 0 0 8.0 0.886500
2 1/1/2015 Quarter1 sweing Thursday 11 0.80 11.41 968.0 3660 50 0.0 0 0 30.5 0.800570
3 1/1/2015 Quarter1 sweing Thursday 12 0.80 11.41 968.0 3660 50 0.0 0 0 30.5 0.800570
4 1/1/2015 Quarter1 sweing Thursday 6 0.80 25.90 1170.0 1920 50 0.0 0 0 56.0 0.800382 
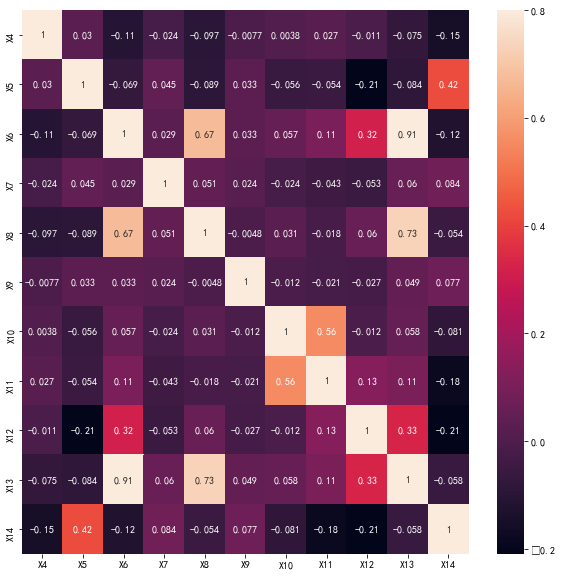
1
2
3
4
5
6
7
import seaborn as sns
plt.rcParams['font.sans-serif']='SimHei'

corr = data[['X0','X1','X2','X3','X4','X5','X6','X7','X8','X9','X10','X11','X12','X13','X14']].corr()
plt.figure(figsize=(10,10))  # 指定宽和高（单位：英寸）
sns.heatmap(corr,vmax=0.8,annot=True) # vmax设置热力图颜色取值的最大值；annot设置是否显示格子数字
plt.show()

output-10-0.png

1
#  可以看出各个特征对期望生产率和实际生产率的影响率差异并不大，所以就有可能是期望的生产率没有切合一定的实际问题才导致的这样的差异
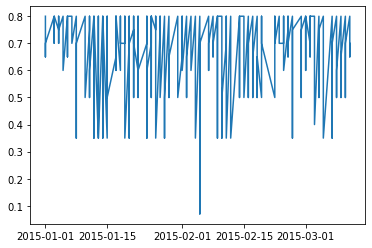
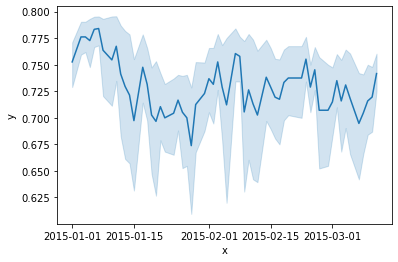
1
2
x = data['X0']
y = data['X5']
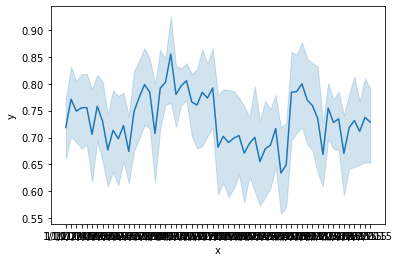
1
2
3
4
5
6
7
8
9
10
plt.plot(x,y)
plt.show()
# seaborn
data= {
    'x':x,
    'y':y
      }
df = pd.DataFrame(data)
sns.lineplot(x='x',y='y',data=df)
plt.show()

output-13-0.png

output-13-1.png

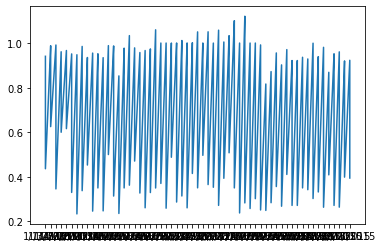
1
2
x = data['X0']
y = data['X14']
1
2
3
4
5
6
7
8
9
10
plt.plot(x,y)
plt.show()
# seaborn
data= {
    'x':x,
    'y':y
      }
df = pd.DataFrame(data)
sns.lineplot(x='x',y='y',data=df)
plt.show()

output-15-0.png

output-15-1.png

1
data.head()
X0 X1 X2 X3 X4 X5 X6 X7 X8 X9 X10 X11 X12 X13 X14
0 1/1/2015 Quarter1 sweing Thursday 8 0.80 26.16 1108.0 7080 98 0.0 0 0 59.0 0.940725
1 1/1/2015 Quarter1 finishing Thursday 1 0.75 3.94 NaN 960 0 0.0 0 0 8.0 0.886500
2 1/1/2015 Quarter1 sweing Thursday 11 0.80 11.41 968.0 3660 50 0.0 0 0 30.5 0.800570
3 1/1/2015 Quarter1 sweing Thursday 12 0.80 11.41 968.0 3660 50 0.0 0 0 30.5 0.800570
4 1/1/2015 Quarter1 sweing Thursday 6 0.80 25.90 1170.0 1920 50 0.0 0 0 56.0 0.800382 
1
data['X4'].unique()
array([ 8,  1, 11, 12,  6,  7,  2,  3,  9, 10,  5,  4], dtype=int64)

1
2
#  一共有12个团队
data1=data.drop(['X0','X1','X2','X3'],axis=1)
1
data1.head()
X4 X5 X6 X7 X8 X9 X10 X11 X12 X13 X14
0 8 0.80 26.16 1108.0 7080 98 0.0 0 0 59.0 0.940725
1 1 0.75 3.94 1039.0 960 0 0.0 0 0 8.0 0.886500
2 11 0.80 11.41 968.0 3660 50 0.0 0 0 30.5 0.800570
3 12 0.80 11.41 968.0 3660 50 0.0 0 0 30.5 0.800570
4 6 0.80 25.90 1170.0 1920 50 0.0 0 0 56.0 0.800382 
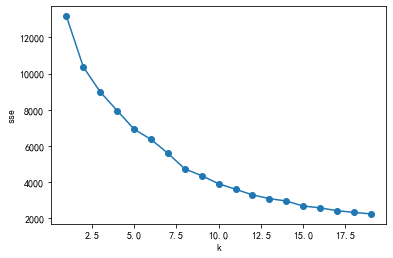
1
2
3
4
5
6
7
8
9
10
11
# 求出簇内误方差
from sklearn.cluster import KMeans
from sklearn.preprocessing import scale
x=pd.DataFrame(scale(data1))
SSE = [] 
k_range = range(1,20)
for k in k_range:
    km = KMeans(n_clusters = k)
    km.fit(x)
    SSE.append(km.inertia_)
SSE
[13167.000000000002,
 10368.001747788787,
 8985.612362104612,
 7956.326143721504,
 6934.1999209667265,
 6364.89500698171,
 5600.08786819714,
 4740.428352871961,
 4360.332443867376,
 3918.830271323268,
 3613.3367590027497,
 3302.354785621584,
 3095.576217636003,
 2963.791234943202,
 2686.863451514291,
 2584.874003399748,
 2427.534059702044,
 2337.8239778345887,
 2250.377455323783]

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
# 然后利用手肘法找出最佳的k值

from sklearn.cluster import KMeans
import matplotlib.pyplot as plt
 
df_features = data1 # 读入数据

# 利用SSE选择k
for k in range(1,20):
    estimator = KMeans(n_clusters=k)  # 构造聚类器
    estimator.fit(df_features[[ 'X4', 'X14']])
X = range(1,20)
plt.xlabel('k')
plt.ylabel('sse')
plt.plot(X,SSE,'o-')
plt.show()

output-21-0.png

1
# 可以看出最佳k值为5
1
data2 = data1[['X4','X14']]
1
2
3
4
5
# k-means 
clf = KMeans(n_clusters=5)
#print(data2)
clf = clf.fit(data2)
clf.labels_
array([4, 0, 3, ..., 4, 1, 4])

1
2
3
#获取中心值
centroids=clf.cluster_centers_
centroids
array([[ 1.50934579,  0.7954856 ],
       [ 9.49019608,  0.72724343],
       [ 3.99317406,  0.75813807],
       [11.52941176,  0.73337501],
       [ 7.05016722,  0.67570864]])

1
2
3
4
5
6
#  用每簇的中心值来代表这一类的水平

columns=['X4', 'X14']
result=pd.DataFrame(centroids,columns=columns)

result
X4 X14
0 1.509346 0.795486
1 9.490196 0.727243
2 3.993174 0.758138
3 11.529412 0.733375
4 7.050167 0.675709 
1
2
3
# 数据归一
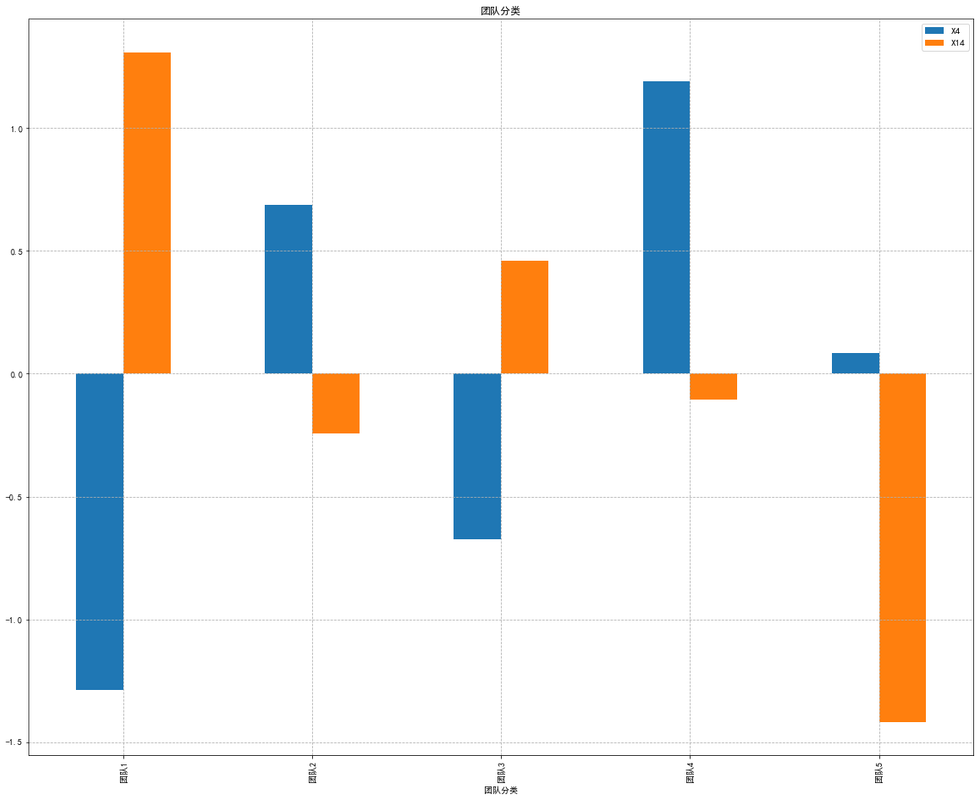
result=(result-result.mean(axis=0))/(result.std(axis=0))
result
X4 X14
0 -1.286294 1.308114
1 0.685944 -0.244505
2 -0.672487 0.458397
3 1.189877 -0.105002
4 0.082961 -1.417004 
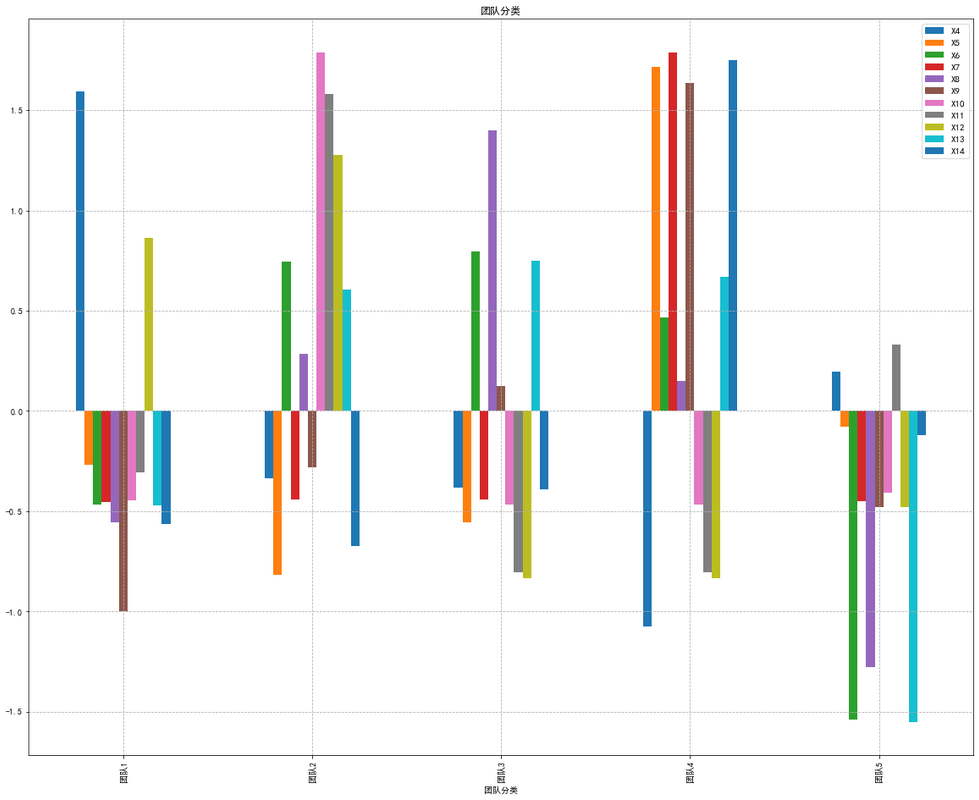
1
2
3
4
5
6
7
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False

result['团队分类']=list(['团队1','团队2','团队3','团队4','团队5']) 
p=result.plot.bar(figsize=(20,16),x='团队分类',title='团队分类',legend='beast')
p.grid(linestyle='--')
p.legend(fontsize=11)
<matplotlib.legend.Legend at 0x290ef9f0940>

output-28-1.png

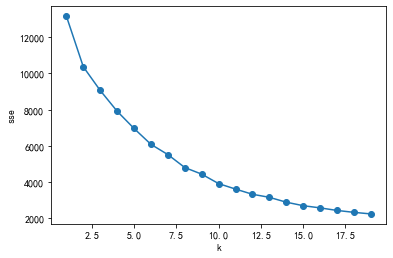
1
2
3
4
5
6
7
8
9
10
# 求出簇内误方差
from sklearn.preprocessing import scale
x=pd.DataFrame(scale(data1))
SSE = [] 
k_range = range(1,20)
for k in k_range:
    km = KMeans(n_clusters = k)
    km.fit(x)
    SSE.append(km.inertia_)
SSE
[13167.000000000002,
 10368.001747788787,
 9059.320705761347,
 7910.63025239119,
 6956.651138200236,
 6077.878903205976,
 5511.898303743294,
 4795.324291351495,
 4429.152799214559,
 3906.8041968464554,
 3603.2482162246365,
 3316.165899966484,
 3147.436870420017,
 2878.2859554852253,
 2684.5121690958435,
 2563.069034412572,
 2421.7083978310657,
 2315.6588424369897,
 2228.865852777383]

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
import pandas as pd
from sklearn.cluster import KMeans
import matplotlib.pyplot as plt
 
df_features = data1 # 读入数据

# 利用SSE选择k
for k in range(1,20):
    estimator = KMeans(n_clusters=k)  # 构造聚类器
    estimator.fit(df_features[[ 'X4','X5','X6','X7','X8','X9','X10','X11','X12','X13','X14']])
X = range(1,20)
plt.xlabel('k')
plt.ylabel('sse')
plt.plot(X,SSE,'o-')
plt.show()

output-30-0.png

1
2
3
4
5
# k-means 
clf = KMeans(n_clusters=5)

clf = clf.fit(data1)
clf.labels_
array([1, 4, 0, ..., 4, 4, 4])

1
2
3
#获取中心值
centroids=clf.cluster_centers_
centroids
array([[ 7.64179104e+00,  7.33582090e-01,  1.41852239e+01,
         9.67542289e+02,  3.75223881e+03,  2.67114428e+01,
         2.23880597e-02,  1.49253731e-01,  2.43781095e-01,
         3.34527363e+01,  7.22864179e-01],
       [ 5.97450425e+00,  7.15212465e-01,  2.35174788e+01,
         1.06944476e+03,  6.65855524e+03,  4.08356941e+01,
         2.37960340e+00,  7.13881020e-01,  3.03116147e-01,
         5.24617564e+01,  7.15187532e-01],
       [ 5.93333333e+00,  7.23939394e-01,  2.39216364e+01,
         1.08087273e+03,  1.05087273e+04,  4.88242424e+01,
         7.77156117e-16,  7.21644966e-16, -1.66533454e-16,
         5.49757576e+01,  7.34676496e-01],
       [ 5.33333333e+00,  8.00000000e-01,  2.13800000e+01,
         1.94093333e+04,  6.19000000e+03,  7.86666667e+01,
         1.11022302e-16,  0.00000000e+00,  0.00000000e+00,
         5.35833333e+01,  8.83637858e-01],
       [ 6.43432203e+00,  7.39830508e-01,  5.93468220e+00,
         1.02024576e+03,  1.25317797e+03,  3.69194915e+01,
         6.25000000e-02,  3.38983051e-01,  5.08474576e-02,
         1.43908898e+01,  7.53440033e-01]])

1
2
3
4
5
6
#  用每簇的中心值来代表这一类的水平

columns=[ 'X4','X5','X6','X7','X8','X9','X10','X11','X12','X13','X14']
result=pd.DataFrame(centroids,columns=columns)

result
X4 X5 X6 X7 X8 X9 X10 X11 X12 X13 X14
0 7.641791 0.733582 14.185224 967.542289 3752.238806 26.711443 2.238806e-02 1.492537e-01 2.437811e-01 33.452736 0.722864
1 5.974504 0.715212 23.517479 1069.444759 6658.555241 40.835694 2.379603e+00 7.138810e-01 3.031161e-01 52.461756 0.715188
2 5.933333 0.723939 23.921636 1080.872727 10508.727273 48.824242 7.771561e-16 7.216450e-16 -1.665335e-16 54.975758 0.734676
3 5.333333 0.800000 21.380000 19409.333333 6190.000000 78.666667 1.110223e-16 0.000000e+00 0.000000e+00 53.583333 0.883638
4 6.434322 0.739831 5.934682 1020.245763 1253.177966 36.919492 6.250000e-02 3.389831e-01 5.084746e-02 14.390890 0.753440 
1
2
3
# 数据归一
result=(result-result.mean(axis=0))/(result.std(axis=0))
result
X4 X5 X6 X7 X8 X9 X10 X11 X12 X13 X14
0 1.595128 -0.266799 -0.468191 -0.455358 -0.555229 -0.997981 -0.445977 -0.304834 0.865386 -0.471215 -0.562291
1 -0.334401 -0.815573 0.744629 -0.442958 0.285093 -0.281737 1.788331 1.583047 1.278707 0.605367 -0.672696
2 -0.382048 -0.554865 0.797153 -0.441567 1.398317 0.123365 -0.467198 -0.803878 -0.832763 0.747749 -0.392407
3 -1.076420 1.717371 0.466842 1.788828 0.149616 1.636681 -0.467198 -0.803878 -0.832763 0.668888 1.749945
4 0.197740 -0.080134 -1.540432 -0.448945 -1.277798 -0.480328 -0.407957 0.329542 -0.478566 -1.550789 -0.122551 
1
2
3
4
5
6
7
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False

result['团队分类']=list(['团队1','团队2','团队3','团队4','团队5']) 
p=result.plot.bar(figsize=(20,16),x='团队分类',title='团队分类',legend='beast')
p.grid(linestyle='--')
p.legend(fontsize=11)
<matplotlib.legend.Legend at 0x290efa33780>

output-35-1.png

1
2
3
#  把时间类型改成datatime类型

data['X0'] = pd.to_datetime(data['X0'], format='%m/%d/%Y')
1
2
3
4
#  设置起始时间
import datetime
start = datetime.datetime(2015,1,1)
end = datetime.datetime(2015,3,1)
1
2
3
subset = data[data['X0']>=start]
data3 = subset[subset['X0']<=end]
data3.shape
(1005, 15)

1
2
#  选出我们要使用的数据
data3
X0 X1 X2 X3 X4 X5 X6 X7 X8 X9 X10 X11 X12 X13 X14
0 2015-01-01 Quarter1 sweing Thursday 8 0.80 26.16 1108.0 7080 98 0.0 0 0 59.0 0.940725
1 2015-01-01 Quarter1 finishing Thursday 1 0.75 3.94 1039.0 960 0 0.0 0 0 8.0 0.886500
2 2015-01-01 Quarter1 sweing Thursday 11 0.80 11.41 968.0 3660 50 0.0 0 0 30.5 0.800570
3 2015-01-01 Quarter1 sweing Thursday 12 0.80 11.41 968.0 3660 50 0.0 0 0 30.5 0.800570
4 2015-01-01 Quarter1 sweing Thursday 6 0.80 25.90 1170.0 1920 50 0.0 0 0 56.0 0.800382
... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ...
1000 2015-03-01 Quarter1 finishing Sunday 2 0.70 3.90 1039.0 960 0 0.0 0 0 8.0 0.585000
1001 2015-03-01 Quarter1 sweing Sunday 7 0.80 30.10 934.0 6960 0 3.5 15 0 58.0 0.579511
1002 2015-03-01 Quarter1 finishing Sunday 1 0.60 3.94 1039.0 3360 0 0.0 0 0 8.0 0.448722
1003 2015-03-01 Quarter1 finishing Sunday 9 0.75 2.90 1039.0 960 0 0.0 0 0 8.0 0.447083
1004 2015-03-01 Quarter1 finishing Sunday 7 0.80 4.60 1039.0 3360 0 0.0 0 0 8.0 0.350417

1005 rows × 15 columns

1
2
3
data3['X2'].unique()

#  一共有三个部门
array(['sweing', 'finishing ', 'finishing'], dtype=object)

1
2
3
4
5
6
#  因为我们更注重实际生产率，所以我们需要观察各个因素对实际生产率的影响

#  通过做corr（）相关系数热力图来查看皮尔逊相关系数比较相关性的大小

# 但是我们可以看出各个因素对实际生产率的影响都不是很大，所以我选择把相关系数大于0.1的因素当成主要因素，当然我们可以考虑把小于0.1的因素去除
#  X7 X8 X9 X10 X13相关系数小于0.1
1
2
data4=data3.drop(['X0','X1','X2','X3'],axis=1)
data4.head()
X4 X5 X6 X7 X8 X9 X10 X11 X12 X13 X14
0 8 0.80 26.16 1108.0 7080 98 0.0 0 0 59.0 0.940725
1 1 0.75 3.94 1039.0 960 0 0.0 0 0 8.0 0.886500
2 11 0.80 11.41 968.0 3660 50 0.0 0 0 30.5 0.800570
3 12 0.80 11.41 968.0 3660 50 0.0 0 0 30.5 0.800570
4 6 0.80 25.90 1170.0 1920 50 0.0 0 0 56.0 0.800382 
1
2
3
4
5
#  处理完后的数据

y = data4.X14.values
X = data4.drop(['X14'], axis = 1)
X.shape
(1005, 10)

1
2
3
4
#  对数据进行分割并进行归一化处理
#  作用：去均值和方差归一化。且是针对每一个特征维度来做的，而不是针对样本。（StandardScaler） 
from sklearn.model_selection import train_test_split
X_train,X_test,y_train,y_test = train_test_split(X,y,random_state=6)  #随机种子6
1
2
3
4
5
6
from sklearn.preprocessing import StandardScaler

standardScaler = StandardScaler()
standardScaler.fit(X_train)
X_train = standardScaler.transform(X_train)
X_test = standardScaler.transform(X_test) 
1
2
3
4
5
6
#模型构建（逻辑回归）

from sklearn.linear_model import LogisticRegression 

log_reg = LogisticRegression()
log_reg.fit(X_train,y_train.astype('int'))
LogisticRegression()

1
2
3
4
5
6
# LogisticRegression的一些参数

LogisticRegression(C=1.0, class_weight=None, dual=False, fit_intercept=True,
          intercept_scaling=1, max_iter=100, multi_class='ovr', n_jobs=1,
          penalty='l2', random_state=None, solver='liblinear', tol=0.0001,
          verbose=0, warm_start=False)
LogisticRegression(multi_class='ovr', n_jobs=1, solver='liblinear')

1
log_reg.score(X_train,y_train.astype('int'))
0.9867197875166003

1
log_reg.score(X_test,y_test.astype('int'))
0.9761904761904762

1
2
3
4
5
6
7
8

from sklearn.metrics import accuracy_score


y_predict_log = log_reg.predict(X_test)

# 调用accuracy_score计算分类准确度（metrices模型评估，指标这里面有accuracy_score这个就是准确率的计算）
accuracy_score(y_test.astype('int'),y_predict_log)
0.9761904761904762

1
2
3
4
5
6
7
8
9
10
#  使用网格搜索找出更好的模型参数
#  param_grid字典或字典列表（参数）
# 下面是构建parameter grid，其结构是key为参数名称，value是待搜索的数值列表的一个字典结构
param_grid = [
    {
        'C':[0.01,0.1,1,10,100],
        'penalty':['l2','l1'],
        'class_weight':['balanced',None]
    }
]
1
2
3
4
from sklearn.model_selection import GridSearchCV

grid_search = GridSearchCV(log_reg,param_grid,cv=10,n_jobs=-1)
# 使用 GridSearchCV 高效调参
1
2
%%time
grid_search.fit(X_train,y_train.astype('int'))
Wall time: 1.69 s





GridSearchCV(cv=10, estimator=LogisticRegression(), n_jobs=-1,
             param_grid=[{'C': [0.01, 0.1, 1, 10, 100],
                          'class_weight': ['balanced', None],
                          'penalty': ['l2', 'l1']}])

1
2
3
#  获取最佳估算器(模型)

grid_search.best_estimator_
LogisticRegression(C=1)

1
2
3
4
LogisticRegression(C=0.01, class_weight=None, dual=False, fit_intercept=True,
          intercept_scaling=1, max_iter=100, multi_class='ovr', n_jobs=1,
          penalty='l2', random_state=None, solver='liblinear', tol=0.0001,
          verbose=0, warm_start=False)
LogisticRegression(C=0.01, multi_class='ovr', n_jobs=1, solver='liblinear')

1
2
3
# 查看最佳分数

grid_search.best_score_
0.9853859649122807

1
2
3
#  查看最佳参数

grid_search.best_params_
{'C': 1, 'class_weight': None, 'penalty': 'l2'}

1
2
log_reg = grid_search.best_estimator_
log_reg.score(X_train,y_train.astype('int'))
0.9867197875166003

1
log_reg.score(X_test,y_test.astype('int'))
0.9761904761904762

1
2
3
4
5
6
7
#查看F1指标
#  F1分数（F1-Score），又称为平衡F分数（BalancedScore），它被定义为精确率和召回率的调和平均数。
#  F1 = 2*（p*r）/(p+r)

from sklearn.metrics import f1_score

f1_score(y_test.astype('int'),y_predict_log)
0.5

1
2
3
4
5

from sklearn.metrics import classification_report


print(classification_report(y_test.astype('int'),y_predict_log))
              precision    recall  f1-score   support

           0       0.98      1.00      0.99       244
           1       0.75      0.38      0.50         8

    accuracy                           0.98       252
   macro avg       0.86      0.69      0.74       252
weighted avg       0.97      0.98      0.97       252

1
2
3
4
5
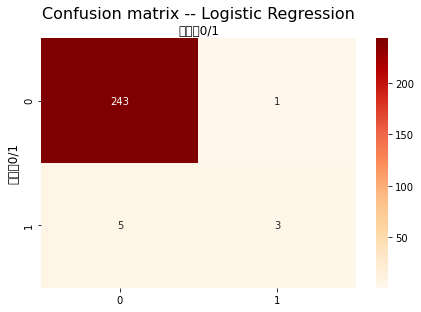
#绘制混淆矩阵（可能性表格或是错误矩阵），评估分类的准确性

from sklearn.metrics import confusion_matrix
cnf_matrix = confusion_matrix(y_test.astype('int'),y_predict_log)
cnf_matrix
array([[243,   1],
       [  5,   3]], dtype=int64)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
def plot_cnf_matirx(cnf_matrix,description):
    class_names = [0,1]
    fig,ax = plt.subplots()
    tick_marks = np.arange(len(class_names))
    plt.xticks(tick_marks,class_names)
    plt.yticks(tick_marks,class_names)

#create a heat map
    sns.heatmap(pd.DataFrame(cnf_matrix), annot = True, cmap = 'OrRd',
               fmt = 'g')
    ax.xaxis.set_label_position('top')
    plt.tight_layout()
    plt.title(description, y = 1.1,fontsize=16)
    plt.ylabel('实际值0/1',fontsize=12)
    plt.xlabel('预测值0/1',fontsize=12)
    plt.show()
    
plot_cnf_matirx(cnf_matrix,'Confusion matrix -- Logistic Regression')

output-63-0.png

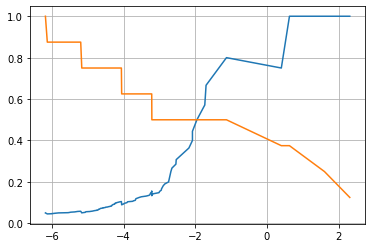
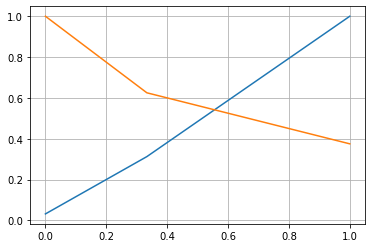
1
2
3
4
5
6
decision_scores = log_reg.decision_function(X_test)
# 数据X上的异常打分，分数越高，则该数据点的异常程度越高

from sklearn.metrics import precision_recall_curve

precisions,recalls,thresholds = precision_recall_curve(y_test.astype('int'),decision_scores)
1
2
3
4
5
6
#  绘制AUC图

plt.plot(thresholds,precisions[:-1])
plt.plot(thresholds,recalls[:-1])
plt.grid()
plt.show()

output-65-0.png

1
2
3
4
5
# 绘制ROC曲线

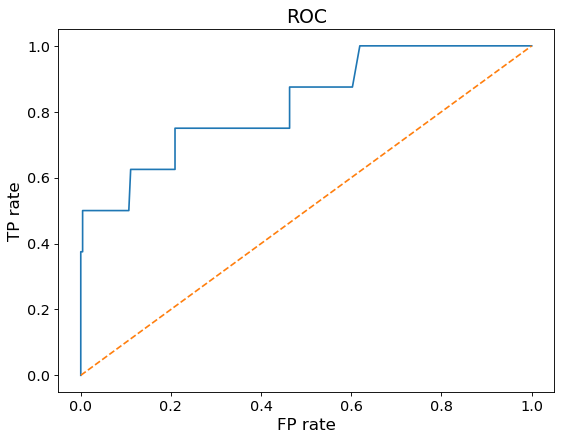
from sklearn.metrics import roc_curve

fprs,tprs,thresholds = roc_curve(y_test.astype('int'),decision_scores)
1
2
3
4
5
6
7
8
9
10
11
12
def plot_roc_curve(fprs,tprs):
    plt.figure(figsize=(8,6),dpi=80)
    plt.plot(fprs,tprs)
    plt.plot([0,1],linestyle='--')
    plt.xticks(fontsize=13)
    plt.yticks(fontsize=13)
    plt.ylabel('TP rate',fontsize=15)
    plt.xlabel('FP rate',fontsize=15)
    plt.title('ROC',fontsize=17)
    plt.show()
    
plot_roc_curve(fprs,tprs)

output-67-0.png

1
2
3
4
# 求面积,相当于求得分（AUC,ROC的面积）
from sklearn.metrics import roc_auc_score  #auc:area under curve

roc_auc_score(y_test.astype('int'),decision_scores)
0.825563524590164

逻辑回归模型得分0.82556

1
2
3
4
5
6
7
8
9
10
11
12
13
#模型创建–KNN临近算法，略过基本模型的创建,直接使用网格搜索进行参数调优

param_grid = [
    {
        'weights':['uniform'],
        'n_neighbors':[i for i in range(1,31)]
    },
    {
        'weights':['distance'],
        'n_neighbors':[i for i in range(1,31)],
        'p':[i for i in range(1,6)]
    }
]
1
2
3
4
5
6
7
%%time
from sklearn.neighbors import KNeighborsClassifier
knn_clf = KNeighborsClassifier()

grid_search = GridSearchCV(knn_clf,param_grid)

grid_search.fit(X_train,y_train.astype('int'))
Wall time: 14.3 s





GridSearchCV(estimator=KNeighborsClassifier(),
             param_grid=[{'n_neighbors': [1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12,
                                          13, 14, 15, 16, 17, 18, 19, 20, 21,
                                          22, 23, 24, 25, 26, 27, 28, 29, 30],
                          'weights': ['uniform']},
                         {'n_neighbors': [1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12,
                                          13, 14, 15, 16, 17, 18, 19, 20, 21,
                                          22, 23, 24, 25, 26, 27, 28, 29, 30],
                          'p': [1, 2, 3, 4, 5], 'weights': ['distance']}])

1
grid_search.best_estimator_
KNeighborsClassifier(n_neighbors=3)

1
2
3
KNeighborsClassifier(algorithm='auto', leaf_size=30, metric='minkowski',
           metric_params=None, n_jobs=1, n_neighbors=24, p=3,
           weights='distance')
KNeighborsClassifier(n_jobs=1, n_neighbors=24, p=3, weights='distance')

1
grid_search.best_score_
0.9840618101545253

1
grid_search.best_params_
{'n_neighbors': 3, 'weights': 'uniform'}

1
2
knn_clf = grid_search.best_estimator_
knn_clf.score(X_train,y_train.astype('int'))
0.9853917662682603

1
knn_clf.score(X_test,y_test.astype('int'))
0.9801587301587301

1
y_predict_knn = knn_clf.predict(X_test)
1
2
3
#  查看F1指标

f1_score(y_test.astype('int'),y_predict_knn)
0.5454545454545454

1
print(classification_report(y_test.astype('int'),y_predict_knn))
              precision    recall  f1-score   support

           0       0.98      1.00      0.99       244
           1       1.00      0.38      0.55         8

    accuracy                           0.98       252
   macro avg       0.99      0.69      0.77       252
weighted avg       0.98      0.98      0.98       252

1
2
3
4
#  绘制混淆矩阵

cnf_matrix = confusion_matrix(y_test.astype('int'),y_predict_knn)
cnf_matrix
array([[244,   0],
       [  5,   3]], dtype=int64)

1
2
# 此处调用前面的绘制函数
plot_cnf_matirx(cnf_matrix,'Confusion matrix -- KNN')

output-82-0.png

1
2
3
4
5
6
7
8
9
10
11
12
#  绘制AUC图

y_probabilities = knn_clf.predict_proba(X_test)[:,1]

from sklearn.metrics import precision_recall_curve

precisions,recalls,thresholds = precision_recall_curve(y_test.astype('int'),y_probabilities)

plt.plot(thresholds,precisions[:-1])
plt.plot(thresholds,recalls[:-1])
plt.grid()
plt.show()

output-83-0.png

1
2
3
4
5
6
#  绘制ROC曲线
from sklearn.metrics import roc_curve

fprs2,tprs2,thresholds = roc_curve(y_test.astype('int'),decision_scores)
# 此处调用前面的绘制函数
plot_roc_curve(fprs2,tprs2)

output-67-0.png

1
2
3
4
# 求面积,相当于求得分
from sklearn.metrics import roc_auc_score  #auc:area under curve

roc_auc_score(y_test.astype('int'),y_probabilities)
0.7984118852459017

KNN模型的得分为0.798411

1
2
3
4
#  模型创建–DecisionTree

from sklearn.tree import DecisionTreeClassifier
dt_clf= DecisionTreeClassifier(random_state=6)
1
2
3
4
5
6
7
8
9
10
11
12
from sklearn.model_selection import GridSearchCV
param_grid = [
    {
        'max_features':['auto','sqrt','log2'],
        'min_samples_split':[2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18],
        'min_samples_leaf':[1,2,3,4,5,6,7,8,9,10,11]
    }
]

grid_search = GridSearchCV(dt_clf,param_grid)

grid_search.fit(X_train,y_train.astype('int'))
GridSearchCV(estimator=DecisionTreeClassifier(random_state=6),
             param_grid=[{'max_features': ['auto', 'sqrt', 'log2'],
                          'min_samples_leaf': [1, 2, 3, 4, 5, 6, 7, 8, 9, 10,
                                               11],
                          'min_samples_split': [2, 3, 4, 5, 6, 7, 8, 9, 10, 11,
                                                12, 13, 14, 15, 16, 17, 18]}])

1
grid_search.best_estimator_
DecisionTreeClassifier(max_features='auto', min_samples_split=9, random_state=6)

1
grid_search.best_score_
0.9814128035320089

1
grid_search.best_params_
{'max_features': 'auto', 'min_samples_leaf': 1, 'min_samples_split': 9}

1
2
dt_clf = grid_search.best_estimator_
dt_clf.score(X_train,y_train.astype('int'))
0.9814077025232404

1
dt_clf.score(X_test,y_test.astype('int'))
0.9761904761904762

1
y_predict_dt = dt_clf.predict(X_test)
1
2
3
#  查看F1指标

f1_score(y_test.astype('int'),y_predict_dt)
0.4

1
print(classification_report(y_test.astype('int'),y_predict_dt))
              precision    recall  f1-score   support

           0       0.98      1.00      0.99       244
           1       1.00      0.25      0.40         8

    accuracy                           0.98       252
   macro avg       0.99      0.62      0.69       252
weighted avg       0.98      0.98      0.97       252

1
2
3
4
#  绘制混淆矩阵

cnf_matrix = confusion_matrix(y_test.astype('int'),y_predict_dt)
cnf_matrix
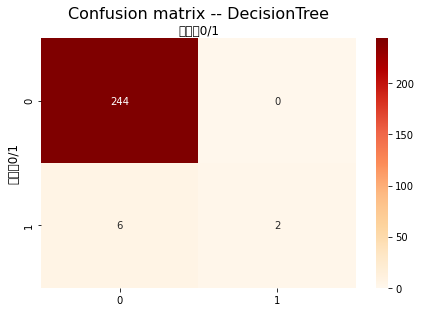
array([[244,   0],
       [  6,   2]], dtype=int64)

1
2
# 此处调用前面的绘制函数
plot_cnf_matirx(cnf_matrix,'Confusion matrix -- DecisionTree')

output-98-0.png

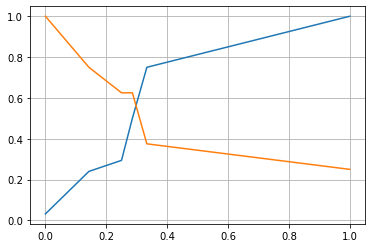
1
2
3
4
5
y_probabilities = dt_clf.predict_proba(X_test)[:,1]

from sklearn.metrics import precision_recall_curve

precisions,recalls,thresholds = precision_recall_curve(y_test.astype('int'),y_probabilities)
1
2
3
4
plt.plot(thresholds,precisions[:-1])
plt.plot(thresholds,recalls[:-1])
plt.grid()
plt.show()

output-100-0.png

1
2
3
4
5
6
#  绘制ROC曲线

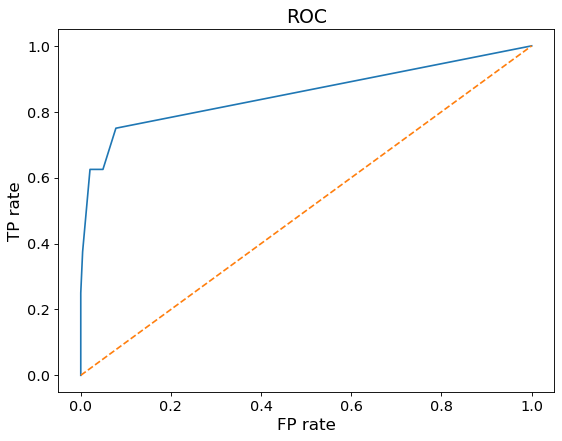
from sklearn.metrics import roc_curve
fprs3,tprs3,thresholds3 = roc_curve(y_test.astype('int'),y_probabilities)
# 此处调用前面的绘制函数
plot_roc_curve(fprs3,tprs3)

output-101-0.png

1
2
3
4
# 求面积,相当于求得分
from sklearn.metrics import roc_auc_score  #auc:area under curve

roc_auc_score(y_test.astype('int'),y_probabilities)
0.8539959016393442

决策树模型的得分为0.85399

1
#  通过对比，我们选择XGboost模型
1
#  利用XGboost来预测数据
1
2
3
#  X7 X8 X9 X10 X13相关系数小于0.1

data5=data3.drop(['X0','X1','X2','X3','X7','X8','X9','X10','X13'],axis=1)
1
data5.head()
X4 X5 X6 X11 X12 X14
0 8 0.80 26.16 0 0 0.940725
1 1 0.75 3.94 0 0 0.886500
2 11 0.80 11.41 0 0 0.800570
3 12 0.80 11.41 0 0 0.800570
4 6 0.80 25.90 0 0 0.800382 
1
#  进行训练和预测
1
2
3
4
5
6
7
8
9
# 为了正确评估模型性能，将数据划分为训练集和测试集，并在训练集上训练模型，在测试集上验证模型性能。
from sklearn.model_selection import train_test_split

## 选择其类别为0和1的样本 （不包括类别为2的样本）
data_target_part = data5['X14']
data_features_part = data5[[x for x in data5.columns if x != 'X14']]

## 测试集大小为20%， 80%/20%分
x_train, x_test, y_train, y_test = train_test_split(data_features_part, data_target_part, test_size = 0.2, random_state = 2020)
1
2
3
4
5
from xgboost.sklearn import XGBClassifier
## 定义 XGBoost模型 
clf = XGBClassifier()
# 在训练集上训练XGBoost模型
clf.fit(x_train, y_train)
1

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
# 在训练集和测试集上分布利用训练好的模型进行预测
train_predict = clf.predict(x_train)
test_predict = clf.predict(x_test)
from sklearn import metrics

## 利用accuracy（准确度）【预测正确的样本数目占总预测样本数目的比例】评估模型效果
print('The accuracy of the Logistic Regression is:',metrics.accuracy_score(y_train,train_predict))
print('The accuracy of the Logistic Regression is:',metrics.accuracy_score(y_test,test_predict))

## 查看混淆矩阵 (预测值和真实值的各类情况统计矩阵)
confusion_matrix_result = metrics.confusion_matrix(test_predict,y_test)
print('The confusion matrix result:\n',confusion_matrix_result)

# 利用热力图对于结果进行可视化
plt.figure(figsize=(8, 6))
sns.heatmap(confusion_matrix_result, annot=True, cmap='Blues')
plt.xlabel('Predicted labels')
plt.ylabel('True labels')
plt.show()
1
2
3
# 利用XGBoost进行特征选择

sns.barplot(y=data_features_part.columns, x=clf.feature_importances_)
1
#调参
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
# 从sklearn库中导入网格调参函数
from sklearn.model_selection import GridSearchCV

## 定义参数取值范围
learning_rate = [0.1, 0.3, 0.6]
subsample = [0.8, 0.9]
colsample_bytree = [0.6, 0.8]
max_depth = [3,5,8]

parameters = { 'learning_rate': learning_rate,
              'subsample': subsample,
              'colsample_bytree':colsample_bytree,
              'max_depth': max_depth}
model = XGBClassifier(n_estimators = 50)

## 进行网格搜索
clf = GridSearchCV(model, parameters, cv=3, scoring='accuracy',verbose=1,n_jobs=-1)
clf = clf.fit(x_train, y_train)
clf.best_params_##网格搜索后的最优参数
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
# 在训练集和测试集上分布利用最好的模型参数进行预测

## 定义带参数的 XGBoost模型 
clf = XGBClassifier(colsample_bytree = 0.6, learning_rate = 0.3, max_depth= 8, subsample = 0.9)
# 在训练集上训练XGBoost模型
clf.fit(x_train, y_train)

train_predict = clf.predict(x_train)
test_predict = clf.predict(x_test)

## 利用accuracy（准确度）【预测正确的样本数目占总预测样本数目的比例】评估模型效果
print('The accuracy of the Logistic Regression is:',metrics.accuracy_score(y_train,train_predict))
print('The accuracy of the Logistic Regression is:',metrics.accuracy_score(y_test,test_predict))

## 查看混淆矩阵 (预测值和真实值的各类情况统计矩阵)
confusion_matrix_result = metrics.confusion_matrix(test_predict,y_test)
print('The confusion matrix result:\n',confusion_matrix_result)

# 利用热力图对于结果进行可视化
plt.figure(figsize=(8, 6))
sns.heatmap(confusion_matrix_result, annot=True, cmap='Blues')
plt.xlabel('Predicted labels')
plt.ylabel('True labels')
plt.show()

大家可以根据以下链接下载信息素养大赛校赛题，每年大同小异，考的基本都是那些，本人在21年参加素养大赛校赛时是刷的20年的题，适用。
此链接永久有效
链接：https://pan.baidu.com/s/1svu1k3AfeZfvsHoTbAs_eg
提取码：8888